Bullet "drop table" data is available in many places, including manufacturers catalogs, internet sites, and the back of packages. Usually these are off-the-shelf commercial bullets with speeds from roughly 1300 to 2800 fps, or Mach 1.2 to Mach 2.5 In reviewing such data for a variety of modern bullets, one sees that in many cases the change in velocity with distance is nearly a straight line. Conceptually we start with a table of velocities versus range at fixed intervals, and find the difference in velocity between each data point. Plot this difference versus the average range for the two points.
Listed are data for one such bullet, an 80 grain Winchester made .243 Winchester, ID=X2431
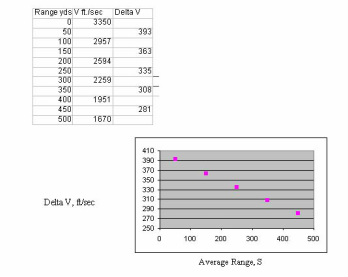
The red dots in the figure are well described by saying that deltaV/deltaS = 2AS + B. For many bullets this relation is accurate to within 5 parts in 10,000. Note that this equation is consistent with the idea that the slowing of the bullet is linearly related to the mass of air moved. Upon integration over S, this becomes our basic equation for velocity versus range:
V = A S^2 + B S + Vz (1)
where A and B are fitting constants, S is the range or distance from the muzzle, and Vz is the velocity at zero distance. To the extent this relation fits the data, it is accurate to say that there is parabolic relation between velocity and distance.
Note too that this equation is based on data, and has implicit within it factors like drag and ballistic coefficients.
Determining the constants A and B from a data set can be done several ways. One is given later on. The most accurate method is a full least squares regression.